We are concerned here with the history of physics which led to Schrödinger’s discovery of the equation bearing his name in 1926. Classical physics had many successes in the two centuries from 1700 to 1900, among them a good understanding of statics (building bridges), gravity, many aspects of electromagnetic radiation (infra-red, light, ultraviolet), and some appreciation of the atomic nature of matter. But (for our purposes) there were two areas where classical physics failed miserably. The first was in understanding certain properties of light, and the second was in understanding the structure of atoms and the spectrum of light they gave off.

The point of giving this history in an article on understanding quantum physics and its implications is to show how a number of different steps led from physics being based on easily visualized and understood particles to physics being based on ‘non-intuitive’ wave functions, which have properties that are difficult to understand.


Thermal Radiation: The first problem had to do with thermal radiation. Suppose you make a box out of copper or any other metal and put a small hole in one side. Then you heat the box to, say 2,500^o F. Electromagnetic radiation, infra-red and visible light, is emitted from the hole and its characteristics can be measured. For example one can filter out all the radiation except that between green and yellow-green and measure how much energy is coming out per second. Then one can do the same thing for all the light between yellow-green and yellow, and so forth. In this way, one can build up the spectrum of the light—how much energy is emitted per second for each color (wavelength). Then one can change the temperature, say to 3,000^o F and repeat the experiment.

This was done with quite good accuracy for many temperatures. It was found that the spectra were identical for different materials, say steel instead of copper. The game of physics was to find a mathematical theory which gave the experimental shape of these curves at all temperatures.

The interesting point is that classical theory failed miserably here; it gave the answer of infinity for the amount of light emitted! This failure occurred because light (electromagnetic radiation) was assumed to have a continuously variable intensity and was thus able to carry a continuously variable amount of energy.

Planck, 1900. Planck attacked the problem first from a purely pragmatic point of view. By intelligent trial and error, he found a relatively simple mathematical formula that fit all the data (energy vs. color for many temperatures). He then found a way to derive this formula by assuming the light did not have a continuously variable intensity. Instead, its energy was quantized; it could only take on the discrete values
where c is the speed of light, is the wavelength of the light, and h is a new constant of nature, now known as Planck’s constant. This assumption, that the energy of light was quantized, then led to the correct curves at all temperatures. Actually, Planck’s ‘model’ was not that the energy of the light was directly quantized but rather that the energies of the atoms making up the container were quantized. And this implied the quantization of light energy.

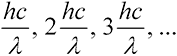
Einstein, the photoelectric effect and photons, 1905. There was a second light-related property of matter that defied explanation by classical physics. If light is shone on a metal surface, electrons will be ejected from the surface. Classically, this should not happen. Only a small part of the light wave hit each (very small) electron and it should have taken many minutes before an electron had acquired enough energy to get bounced out of the metal. But the effect—electrons being emitted from the metal—was essentially instantaneous.

To explain this, Einstein used Planck’s idea of quantization, but he applied it directly to the light (rather than to the atoms in the container). He assumed, in stark contrast to the classical, continuous model, that light was concentrated in localized ‘bundles,’ essentially particles, which we now know by the name of photons. Each photon had energy hcl . Conservation of energy then gave exact agreement with the experimental results (on the energy of the emitted electrons).

Compton scattering of x-rays, 1923. Einstein’s explanation was not immediately accepted. To test the light-as-particle idea, Compton scattered (bounced) x-rays off electrons. The wavelengths of the x-rays were shifted slightly when they bounced off the electrons, and the measured result agreed exactly (within experimental error) with the predictions of Einstein’s photon theory of light, thus providing ‘irrefutable’ evidence that light did indeed consist of tiny localized particles of energy hcl.

Quantum physics. At this point we will step out of historical sequence to consider the relation of quantum physics (discovered later, in 1926) to the photoelectric effect and Compton scattering. The principles used to successfully derive the results were: that the electron was a very small particle which carried classical energy and momentum; that the photon was a very small particle that carried energy hcl and momentum hl ; and conservation of energy and momentum.

Now we know from group representation theory (see Mass, Spin, Charge and the Wave Function and No Evidence for Particles) that wave functions carry energy and momentum, and that energy and momentum are also conserved in quantum physics. Further we know that, in contrast to the classical case, a small part of the photon wave function carries the full energy and momentum (see Small Parts). These are sufficient to derive the photoelectric effect and Compton scattering results from quantum physics alone; the hypothesis of particulate photons (and electrons) is not necessary!

Instability. Discrete wavelengths. Classical physics also failed in two ways to account for properties of the atom. First, there was no way to understand the stability of the atom. No matter how you distributed classical charges, the atom was always unstable. Second, when suitably stimulated by an electric discharge, atoms give off light. But this light is not a continuum of colors, as occurs in the light from the sun. Instead, just a few colors are given off. Further, it was found that the several dozen wavelengths—accurately measured to better than 1 part in a million—given off by the hydrogen atom could be expressed in a simple formula; That is, you put in an integer for n_ƒ and a larger integer for n_i, and you get one of the wavelengths of light emitted by hydrogen. Classical physicists had no clue about how to explain this discrete (not continuous) spectrum.

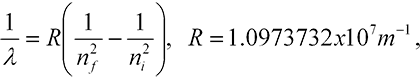
Rutherford, scattering experiments, structure of the atom, 1911. Instead of trying to figure out theoretically what the structure of a stable atom was, Rutherford devised an elegant way to experimentally probe the structure. He shot alpha particles—helium nuclei spit out in radioactive decays—at atoms and watched how they bounced off the atoms. The only way to understand the result was to assume all the positive charge of the atom (what we now know as the nucleus) was concentrated within a very small region.

This didn’t help the classical position, however, because one still couldn’t construct a stable atom. If you put a point electron in an orbit around the point nucleus, the electron would (classically) spiral into the nucleus in a short time.

The Bohr atom, 1913. Bohr used a strange mixture of classical and non-classical ideas to obtain equation (5-2). He supposed the nucleus of the hydrogen atom was a heavy positively charged point particle and the electron was a light negatively charged point particle that orbited the nucleus. As we said, this leads to an unstable atom. The primary idea that Bohr introduced was that there were special orbits such that the angular momentum was an integer multiple, n_p, of Planck’s constant, h, divided by 2π . This gave a discrete series of allowed energy levels for the electron, with the energy proportional to 1/ n_p².

Further, Bohr supposed that light was emitted when an electron fell from an orbit with a higher energy to one with a lower energy, and the difference in energies was the energy of the emitted light. Bohr then used the Planck-Einstein idea that the energy of a photon is hcl.

Putting all these together then gave equation (5-2) for the possible values of the wavelengths of light emitted by hydrogen. The n_i comes from the initial orbit of the electron and the n_f from the final orbit. The constant R is given in Bohr’s model in terms of the mass and charge of the electron, Planck’s constant, the speed of light, and one other constant from electromagnetic theory. All these numbers were known and they gave exactly the value for R (to within experimental error) in equation (5-2)!

de Broglie, 1923. Although it worked very well, the problem with the Bohr atom was that there was no justification for the ‘special orbit’ condition. de Broglie suggested that, just as there was a particle associated with a light wave (Einstein), so there might be a wave associated with the particulate electron. He then further suggested that an integer number of wavelengths of the wave must fit into any stable orbit of the electron. Finally, he then used the relation between momentum and wavelength that holds for light, and this gave the Bohr special-orbit condition.

In summary, de Broglie’s idea gave a ‘justification’ of Bohr’s special orbit assumption based on the idea that there is a wave associated with a particle.

Schrödinger, 1926. Schrödinger, reasoning from de Broglie’s suggestion, thought that if there was a wave ‘associated with’ a particle, then there must be an equation for that wave. Then, using an educated guess based on the total energy being a sum of kinetic and potential energies, and with a very solid grounding in mathematical physics, he found a (linear, partial differential) equation which gave the correct (Bohr) answers for the energy levels of the hydrogen atom.

Only now, there were no unexplained assumptions such as Bohr’s special orbit condition. One simply had this equation, and its answers gave the correct energy levels. Further, this equation could be generalized to more complicated atoms (which the Bohr model could not) and it gave the correct energy levels (and discrete light spectrum). This in effect solved all the problems with light and atoms that had so vexed classical physics.

Waves vs. particles. But in solving those problems, the Schrödinger equation—virtually synonymous with quantum physics—introduced a host of problems of its own. The initial conceptual picture—and it continues somewhat down to the present day—is that the wave function is ‘associated with’ a particle. But we see in No Evidence for Particles and the ideas leading up to that section that there is no justification for this conceptual picture. And if the ‘associated particle’ picture is dropped, most of the mysteries of quantum physics simply go away.


The other great physics idea of the early 1900s was Einstein’s relativity. It did not have much influence on the evolution of the ideas that ended up with the Schrödinger equation. But it has one consequence that is very important for showing that wave functions give a particle-like physical universe. The group-theoretic arguments of the section Mass, Spin, Charge and the Wave Function show that relativity implies mass, energy, momentum, and (quantized) spin are properties of the wave function.


The physicists of the early 1900s were committed to finding mathematical-conceptual pictures of physical reality which could explain the experimental results. This led them to a view of physical reality—it is built from wave functions—that would almost certainly never have been thought of if the experiments that probed the properties of matter had never been done, or if the physicists had continued to think of the physical universe strictly in terms of classical, everyday concepts.

To me, the Schrödinger equation is the most profound discovery in science. It opens a door to a vista on physical reality that we would not have otherwise known about.

Note: Heisenberg was an influential figure in the early years of quantum physics. In fact, he found a different (but equivalent) form of quantum physics a year before Schrödinger. But it is Schrödinger’s form which is of interest here.