The primary characteristic of quantum physics is that it is linear. Therefore it is logical to ask whether mathematical collapse can fit within a linear theory. We find that it cannot; the probability law requires a mathematical collapse to be non-linear.

Non-unitary time translation. If the Hamiltonian H is Hermitian (so time translation is unitary), as it is in conventional theory, then the norms of the different branches of the wave function stay the same forever. So there can be no collapse if one sticks to a linear, unitary theory. But what would happen if we kept the Hamiltonian linear but allowed it to be non-Hermitian so that time translation is no longer unitary? Suppose in particular that some part of the Hamiltonian can change the norm of the wave function, with the change depending on the random variables w, where the choice of w’s at each stage in the time evolution is independent of the coefficients (linearity). Then we have for the general linear case, with O being the time translation operator,
where the conjectured Hamiltonian is presumed to have no effect on the ‘shape’ of the wave function (and we have ignored the non-collapse part of the Hamiltonian). In this case, it might happen that after some time has elapsed, for some value of i,
so we end up with a system which has collapsed to state i. Thus linearity does not rule out collapse.

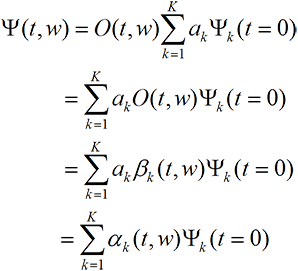
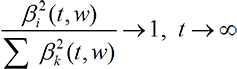
The |a(i)|² probability law requires collapse to be non-linear. But now suppose the collapse follows the |ai|² probability law. Then for large t and given i, Eq. (22A-2) will hold (depending on the sequence of w’s chosen) a fraction |ai|² of the time and the same equation with 1 replaced by 0 will hold the rest of the time. Thus to satisfy the |a(i)|² probability law, the average (averaged over the choice of w’s) of the ratio must obey
where P is the probability of a certain set of w’s, and the integral over all possible w’s is suitably defined. If P(w) is independent of the coefficients, this cannot hold because the left hand side has no dependence on the a_i. Thus to satisfy Eq. (22A-3), P(w) must depend on the coefficients.

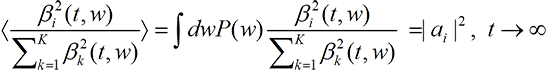
Suppose now we think of numerically integrating the equation of motion, including the w-dependent random part, step by small step. At each step in the integration, the choice of w’s dictated by depends on the coefficients. And then the dependence of the Hamiltonian on the w’s gives an indirect dependence of the Hamiltonian on the coefficients, so that different initial a_i's will produce different w’s. But then
and so the equations of motion are non-linear, in contrast to current quantum physics.