To see how this leads to the |a(i)|² probability law, suppose we do a spin Stern-Gerlach Experiment N times, with N large. The amplitude for spin (+ ) is a₁ and that for spin (-) is a₂. Then if the observer observes only the end result—and not the intermediate ones—the amplitude squared for perceiving m (+ ) spins and N – m (-) spins is
A simple calculation using Stirling’s approximation for the factorials shows that the amplitude squared has a sharp maximum, as a function of m, at m=N|a₁|², so the amplitude squared for m near the maximum is much larger than the amplitude squared for m not near the maximum. Thus according to property 6, the perceived result will have m near the maximum at N|a₁|².

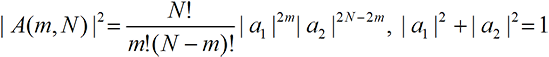
Probability test of the Mind-Mind interpretation. In the Mind-MIND interpretation, we note that the probability law for long runs holds in the Mind-MIND interpretation only if individual results are not observed. This is most interesting because it implies this conjectured origin of the probability law can be experimentally tested. Suppose the Stern-Gerlach (or some other) experiment is carried out in such a way that the observer perceives the outcome of every run. Then if the above holds, it is possible, indeed likely, that after many runs of the experiment, the average value of m/N could be relatively far from |a₁|².


1. The MIND must perceive the magnitude of the coefficients. There is one more observation here. In the last problem considered in Details of Observer-Induced Collapse, we noted that, to obtain information on the coefficients, the collapsing ‘mechanism’ must ‘perceive’ the whole wave function, not just that of the brain. In our scheme, this means that for events external to the brain—Schrödinger’s cat, nuclear decay—it must be the overarching MIND that perceives the whole wave function and then decides which version to concentrate on. (Remember there is no collapse here, so no interference effects inadvertently get wiped out.) But the individual Mind—a restricted aspect of the MIND—can still perceive just the brain wave function and then decide on which internal state of the brain (that is, which thought) to concentrate on.

2. The Many-Minds Interpretation. In the many-minds interpretation of Albert and Loewer (see Ref. 6) there is a continuous infinity of minds associated with each observer. Each of these minds chooses to perceive one or the other branch at random, according to the |a(i)|² probability law. And so, assuming our current perceptions correspond to those of one of the continuous infinity of minds, we would seem to arrive at the probability law—our perceptions are more likely to correspond to a state with large |a(i)|² because more minds have chosen that state.

But that is not correct. Suppose we have a two-state system with |a(1)|²=.2 , |a(2)|²=.8. There is a continuous infinity of minds that perceive each outcome. But even though four minds choose state 2 for every one that chooses state 1, the same number of minds choose each. Why? Because of the way infinities work; four times infinity is still just infinity. Or to say it another way, there are the same number, , of points on a line from 0 to .2 as there are on a line from .2 to 1. Thus, because the ‘same number’ of minds perceives each possibility, the many-minds interpretation cannot account for the probability law.

3. Mindless hulks. One of the main reasons Albert and Loewer proposed their complex many-minds scheme was to avoid mindless hulks—versions of the observer with no associated Mind. But I don’t see them as a problem. The ‘enlivening’ principle in a being is the non-physical Mind. When the Mind does not focus on a particular version of the observer, that version reverts to the same status as any other mindless object, such as a detector; it just evolves according to quantum mechanical laws. The same is true, of course, for the “Minded” version. But the Mind associated with the “Minded” version keeps making decisions about which branch constitutes ‘reality,’ and that is what makes it alive. The Mind is “the fire in the equations .” (Actually it is the fire outside the equations.) Note that we have no sentient beings (the version ‘inhabited’ by the Mind) talking to mindless hulks (the versions not inhabited) in the Mind-MIND interpretation because each individual Mind and the overarching MIND all concentrate on the same version.

4. Non-standard probability. How could the perceived results of many runs of the Stern-Gerlach experiment always be near m/N=|a_i|² if just the end result is perceived, but not near that value if every intermediate result is perceived? It does not arise because the non-physical Mind is influencing the outcome of each event (there is, in fact, no ‘outcome of each event’ because all the versions of reality continue forever). To see what is happening, suppose the ‘probability law’ for the Mind perceiving event i is s(x)=x+.1(x)(1-x)(.5-x) where x is the amplitude squared. Then if each individual result is observed, the value for m/N will be near s(x),x=|a₁|² , in disagreement with the |a_i|² probability law. But if only the end result is observed, the value for m/N will be the one that maximizes s(x) where x is the appropriate amplitude squared,
From Stirling’s approximation for the factorial and the chain rule for derivatives, we find this gives a maximum at m/N=|a_i|², in agreement with the |a_i|² probability law.

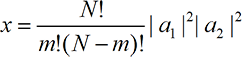
5. The Rutherford Experiment. One might suspect that experiments in which every outcome is observed have already been done. In particular, suppose we consider the original (1911) Rutherford scattering experiment, where a flash of light was observed (by a graduate student using a microscope) every time a decay particle hit the zinc sulfide detector. This experiment won’t do as a test of the probability law, however, because not every outcome is observed. Only that very small fraction of events where the decay particle hits the small detector is observed. And one can show in that case that the |ai|² law will indeed hold (except perhaps for an overall normalization factor) no matter what the ‘probability law’ is for the perception of individual events.

To sketch the argument, suppose we do a scattering experiment in which there are R scattering events per second, but we observe only those events which register in a very small solid angle. Then one can prove that the scattering amplitudes squared are, to a good approximation, functions of the product Rt|a_i|² rather than being functions of |a_i|² and Rt separately, where t is the time the experiment has been run, and a_i is the amplitude for scattering into solid angle i. This implies that, independent of the functional dependence of probability on |a_i|² , the average time for observing a single event i is proportional to 1/(R|a_i|²), which is exactly the result one obtains if the probability law is ||a_i|². Thus the individually observed scattering events in the original Rutherford experiment give no information on the specific probability law.