Principles and Concepts
of Quantum Physics
of Quantum Physics
Implications of
Quantum Physics
Quantum Physics
8A. Details of Separate, Isolated Universes.
Summary
The different versions of reality in the wave function, such as Schrodinger’s cat alive or Schrodinger’s cat dead, are in separate universes, with no communication possible between the universes.
We will show that the different versions of reality in the wave function are in separate universes which cannot affect each other in any way as time progresses. This result is demonstrated using a particular example, but the same arguments would hold whenever any ‘single-particle’ wave function (except perhaps that for a photon) simultaneously takes at least two different paths. It depends on the linearity of the theory.
Fire a spin
Now consider the Schrödinger equation for the full wave function (including both versions of reality) describing the silver atom and the detectors;
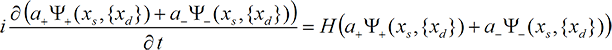
where the a’s give the relative sizes of the two versions, xs is the coordinate of the silver ‘atom’ and { xd } represents the coordinates of all the ‘atoms’ in the detectors (plus the observer if one wishes).
(Note: The H inEqs. (8A-1), (8A-2) and (8A-3) imply the wave functions for the two branches obey their own separate equations of motion,does not (substantially) change the location of the silver atom. Thus
in Eq. (8A-2) is a function of xs which has the value 0 when xs is not in
.)
(and the Schrödinger equation is irrelevant (0=0) when xs is in neither region.) Thus, because they obey their own separate equations, and because H is independent of the wave function in a linear theory, the evolution of
Further, we see that, once the two parts of the silver atom wave function have separated the coefficients a+ and a- can never change (in a unitary theory). See also Mathematical Collapse and Linearity on the need for non-linearity in mathematical collapse theories.

